- Pengarang Matthew Elmers [email protected].
- Public 2023-12-16 22:16.
- Terakhir diubah 2025-01-24 09:27.

Apa yang menentukan akurasi - salah satu karakteristik utama senjata? Jelas, dari kualitas laras dan cartridge. Mari kita tunda kartrid untuk saat ini, tetapi pertimbangkan fisika prosesnya.
Ambil batang atau tabung logam yang terbuat dari logam elastis dan kencangkan dengan kuat di dasar yang besar. Jadi kami mendapatkan model perangkat yang sedang dipelajari. Sekarang, jika kita memukul batang, tidak masalah di tempat dan ke arah mana, menariknya kembali, atau menekannya, atau, akhirnya, memasukkan kartrid ke dalam tabung dan menembakkan tembakan, kita akan melihat bahwa batang (barel) telah mengalami gerakan osilasi teredam. Getaran ini didekomposisi menjadi yang paling sederhana, dan setiap jenis getaran laras yang begitu sederhana akan mempengaruhi akurasi (keakuratan) pemotretan dengan caranya sendiri.
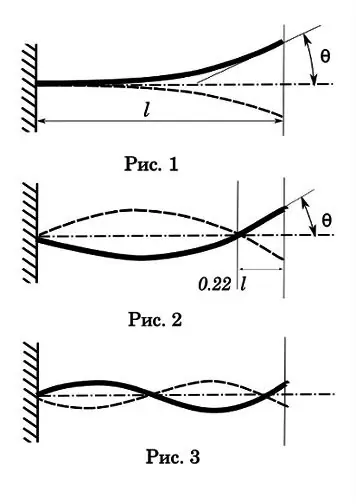
Mari kita mulai dengan getaran orde pertama atau nada. Seperti yang Anda lihat (Gbr. 1), osilasi seperti itu hanya memiliki satu simpul pada titik perlekatan, amplitudo terbesar, waktu peluruhan terlama, dan waktu osilasi terlama dalam satu periode. Kali ini 0,017-0,033 detik. Waktu tempuh peluru melalui lubang adalah 0, 001-0, 002 detik. Artinya, secara signifikan lebih kecil dari siklus satu osilasi, yang berarti bahwa jenis osilasi ini tidak memiliki pengaruh yang signifikan terhadap akurasi satu tembakan. Tetapi dengan pemotretan otomatis, gambar yang menarik dapat dihasilkan. Katakanlah laju api adalah 1200 rds / menit, mis. waktu satu siklus - 0,05 detik. Dengan periode osilasi orde pertama 0, 025 detik, kita memiliki rasio frekuensi berganda. Dan ini adalah kondisi yang sangat diperlukan untuk resonansi dengan semua konsekuensi berikutnya - senjata mulai bergetar dengan kekuatan sedemikian rupa sehingga dapat hancur berantakan.
Mari kita beralih ke osilasi orde kedua (Gbr. 2). Tetapi saya menyarankan agar mahasiswa humaniora terlebih dahulu melakukan eksperimen untuk menghilangkan kekurangan pendidikan di bidang fisika. Anda perlu mengambil anak laki-laki (Anda bisa perempuan), meletakkannya di ayunan dan ayunan. Sebelum Anda adalah pendulum. Berdiri di sisi ayunan dan coba pukul anak itu dengan bola. Setelah serangkaian upaya, Anda akan sampai pada kesimpulan bahwa cara terbaik untuk memukul adalah ketika target berada pada fase osilasi pertama - deviasi maksimum dari titik ekuilibrium. Pada titik ini, target memiliki kecepatan nol.
Mari kita lihat diagram orde kedua. Node getaran kedua terletak sekitar 0,22 dari ujung laras. Titik ini adalah hukum alam, tidak mungkin untuk membuat getaran seperti itu untuk balok kantilever sehingga simpul kedua jatuh di ujung bebas. Di sinilah tempatnya dan tidak tergantung pada panjang laras.
Amplitudo osilasi untuk skema orde kedua lebih rendah, tetapi waktu osilasi sudah sebanding dengan waktu lintasan peluru melalui lubang - 0, 0025-0, 005 detik. Jadi untuk pemotretan tunggal ini sudah menarik. Untuk memperjelas apa yang sedang kita bicarakan, bayangkan sebuah tong sepanjang 1 meter. Peluru bergerak melalui seluruh laras dalam 0,001 detik. Jika periode osilasi adalah 0,004 detik, maka pada saat peluru meninggalkan laras, laras akan mencapai tikungan maksimum pada fase pertama. Pertanyaan untuk kemanusiaan adalah - pada titik apa (dalam fase apa) yang terbaik untuk menembakkan peluru keluar dari laras untuk memastikan konsistensi hasil? Ingat ayunannya. Pada titik nol, vektor kecepatan defleksi batang maksimum. Lebih sulit bagi peluru untuk mengenai titik ini pada potongan laras, ia juga memiliki kesalahan dalam kecepatannya sendiri. Artinya, momen terbaik bagi peluru untuk terbang adalah ketika laras berada pada titik tertinggi fase defleksi pertama - seperti pada gambar. Kemudian penyimpangan yang tidak signifikan dalam kecepatan peluru akan dikompensasi dengan waktu yang lebih lama yang dihabiskan oleh laras dalam fase paling stabilnya.
Representasi grafis dari fenomena ini dapat dilihat dengan jelas pada diagram (Gbr. 4-5). Di sini - t adalah kesalahan waktu saat peluru melewati moncong laras. dalam gambar. 4 ideal ketika waktu lepas landas peluru rata-rata bertepatan dengan fase nol dari osilasi laras. (Ahli matematika! Saya tahu bahwa distribusi kecepatan adalah non-linier.) Daerah yang diarsir adalah sudut penyebaran lintasan.
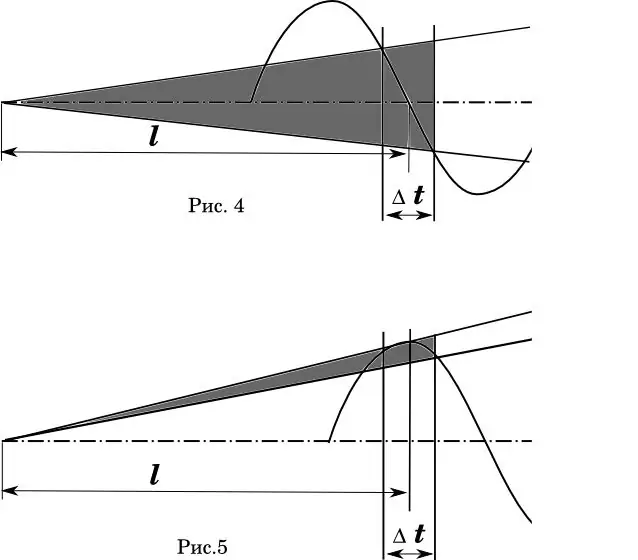
Pada Gambar 5, panjang laras dan kesalahan kecepatan tetap sama. Tetapi fase pembengkokan laras digeser sehingga waktu keberangkatan rata-rata bertepatan dengan defleksi maksimum laras. Apakah komentar berlebihan?
Nah, apakah itu sepadan dengan lilinnya? Seberapa parah penyimpangan yang disebabkan oleh osilasi orde kedua? Serius dan sangat serius. Menurut profesor Soviet Dmitry Aleksandrovich Ventzel, dalam salah satu percobaan, hasil berikut diperoleh: jari-jari deviasi median meningkat 40% dengan perubahan panjang laras hanya 100 mm. Sebagai perbandingan, pemrosesan barel berkualitas tinggi hanya dapat meningkatkan akurasi sebesar 20%!
Sekarang mari kita lihat rumus untuk frekuensi getaran:
di mana:
k - koefisien untuk osilasi orde kedua - 4, 7;
L adalah panjang laras;
E adalah modulus elastisitas;
I adalah momen inersia penampang;
m adalah massa batang.
… dan lanjutkan ke analisis dan kesimpulan.
Kesimpulan yang jelas dari Gambar 4-5 adalah kesalahan kecepatan peluru. Itu tergantung pada kualitas bubuk dan berat serta kepadatannya di dalam kartrid. Jika kesalahan ini setidaknya seperempat dari waktu siklus, maka segala sesuatu yang lain dapat dihentikan. Untungnya, sains dan industri telah mencapai stabilitas yang sangat besar dalam hal ini. Dan untuk yang lebih canggih (di bangku, misalnya) ada semua kondisi untuk perakitan sendiri kartrid untuk menyesuaikan fase pelepasan peluru persis dengan panjang laras.
Jadi, kami memiliki kartrid dengan variasi kecepatan serendah mungkin. Panjang laras dihitung berdasarkan berat maksimumnya. Pertanyaan tentang stabilitas muncul. Kita lihat rumusnya. Variabel apa yang mempengaruhi perubahan frekuensi osilasi? Panjang barel, modulus elastisitas dan massa. Laras memanas saat menembak. Bisa panas mengubah panjang laras sehingga akurasi terpengaruh. Iya dan tidak. Ya, karena angka ini terletak dalam seperseratus persen untuk suhu 200 C. Tidak, karena perubahan modulus elastisitas baja untuk suhu yang sama adalah sekitar 8-9%, untuk 600C hampir dua kali lipat. Artinya, berkali-kali lebih tinggi! Laras menjadi lebih lembut, fase lentur laras bergeser ke depan saat peluru keluar, akurasi turun. Nah, apa yang dikatakan seorang analis yang bijaksana? Dia akan mengatakan bahwa tidak mungkin untuk mendapatkan akurasi maksimum pada panjang satu barel dalam mode dingin dan panas! Senjata itu mungkin memiliki kinerja yang lebih baik dengan laras dingin atau panas. Dengan demikian, dua kelas senjata diperoleh. Salah satunya adalah untuk tindakan penyergapan, ketika target harus dipukul dari tembakan "dingin" pertama, karena akurasi yang kedua akan lebih buruk karena pemanasan laras yang tak terhindarkan. Dalam senjata seperti itu tidak ada kebutuhan mendesak untuk otomatisasi. Dan kelas kedua adalah senapan otomatis, yang panjang larasnya disesuaikan dengan laras panas. Dalam hal ini, kemungkinan meleset karena akurasi tembakan dingin yang rendah dapat dikompensasikan dengan tembakan cepat berikutnya yang lebih panas dan lebih akurat.
EF Dragunov mengetahui fisika proses ini dengan sangat baik ketika dia merancang senapannya. Saya sarankan Anda membiasakan diri dengan kisah putranya Alexei. Tapi pertama-tama, seseorang harus mematahkan otak mereka. Seperti yang Anda ketahui, dua sampel Konstantinov dan Dragunov mendekati final kompetisi untuk senapan sniper. Para desainer berteman dan saling membantu dalam segala hal. Jadi, senapan Konstantinov "disetel" ke mode dingin, senapan Dragunov ke "panas". Mencoba meningkatkan akurasi senapan lawan, Dragunov menembakkan senapannya dengan jeda yang lama.

Mari kita lihat lagi rumusnya. Seperti yang Anda lihat, frekuensinya juga tergantung pada massa laras. Massa batang adalah konstan. Tapi kontak keras dengan forend menghasilkan umpan balik positif yang tidak terduga ke laras. Sistem - laras-depan-lengan (penopang) akan memiliki momen inersia yang berbeda (satu set massa relatif terhadap titik lampiran), yang berarti bahwa ini juga dapat menyebabkan pergeseran fasa. Inilah sebabnya mengapa atlet menggunakan dukungan lunak. Fitur yang sama dikaitkan dengan penerapan prinsip "laras yang ditangguhkan", ketika ujung senjata tidak memiliki kontak yang keras dengan laras dan melekat erat padanya (senjata) hanya di area laras. penerima, dan ujung kedua tidak menyentuh laras sama sekali atau menyentuh melalui sambungan pegas (SVD).
Pikiran terakhir. Fakta bahwa dengan panjang laras yang sama tidak mungkin memperoleh akurasi yang sama pada suhu yang berbeda memberikan alasan yang sangat baik untuk meregangkan otak Anda. Anda hanya perlu mengubah panjang dan / atau massa laras ketika suhu laras berubah. Tanpa mengubah panjang atau berat laras. Dari sudut pandang humaniora, ini adalah paradoks. Dari sudut pandang teknisi, tugas yang ideal. Seluruh kehidupan seorang desainer terhubung dengan solusi dari masalah seperti itu. Sherlock sedang beristirahat.






